In the era of computer science, managing and handling data is important to build powerful and adaptable applications. There are various data structures available to manage and organize data. 

An array in data structure is a collection of elements that are of the same data type, where each element is uniquely accessed using its corresponding index . It is a basic building block to understand complex data structures.

Whether you are a beginner or experienced developer (working professional) understanding complexity analysis and optimizing solutions is key. 

In this article we will focus on understanding array in data structure , exploring their types, representation of arrays in memory, several operations performed on arrays, complexity analysis, advantages & disadvantages of arrays.

What is Array in Data Structure ?

An array in data structure is a collection of elements that are of the same data type, where each element is uniquely accessed using its corresponding index. Elements in arrays having the same data type whether it’s integer, float and character. All elements in an array are stored in a consecutive memory location and the size of the array in data structure remains fixed during the declaration (i.e., you can’t shrink or grow array size till the execution of the program ).

Example : –  1) int arr_example [6] = { 56, 92, 38, 97, 90, 89} (Array of integers)

Here, ‘int’ keyword represents that the array is of integer type , ‘arr_example’ represents the name of an array. This array consists of all integer elements and it is of fixed size (6).

Array represents order in two forms i.e, column major order and row major order. These orders in an array are important when we go for multi-dimensional arrays to place elements like the way we represent the order of an array.

Types of Arrays in Data Structure 

There are different types of arrays in data structure that define according to the dimension. In this article we will mainly cover three types : 

Linear Dimensional Array in Data Structure (1D)

In a linear dimensional array data structure elements are arranged linearly and each element can be accessed using its corresponding index.

Example : 1) int arr_example[6]={56, 92, 38. 97, 90, 89}

               2) int arr_example[9]={ 77, 67, 90, 88, 12, 34, 09, 08, 12}

Two-Dimensional Array in Data Structure (2D)

Elements in a two-dimensional array should be structured in the form of table i.e rows and columns. It’s like the way you represent elements in a matrix form.

In this example mentioned above, every element is arranged in the form of a table (i.e, in rows and columns).

Multiple Dimensional Array in Data Structure

Multiple dimensional  arrays are the extended part of a two-dimensional array. Here we are using more than two dimensions (i.e, 3D , 4D arrays).

Example : 3D array [a][b][c].

Memory Allocation of Arrays 

Array in data structure stores elements in a contiguous memory location and each element has its unique index for representation. Elements of an array in data structure are accessed by their unique indices (i.e, every element has their own index ) during compile-time.

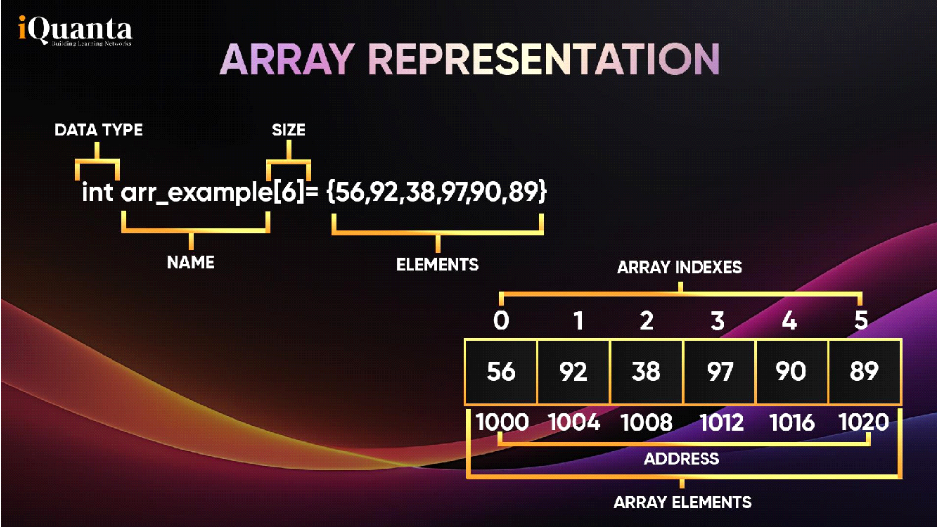
As represented in the image above, the first block of arr_element  having index ‘0’ and arr_example[0] also represents the base address (i.e., memory address of the first element).

In the similar way every element in the arr_example array has their unique index which is represented by an integer value and the index number of the first element starts with ‘0’ like the way it is represented in the image.

Every element has its own unique address and the address allocation in 1D array is calculated as: 

Address of arr_example[ p ] = base address + ( p * size of each element ) [Address Allocation]

In this address allocation form mentioned above ‘ p ‘ represents the index of the element in an array.

Example : arr_example[ 0 ] = 1000

               arr_example[ 5 ] = 1020

Operations on an Array in Data Structure 

Search Operation (Searching)

A Searching operation in an array is used to find a particular element .

Example : arr_example [6] = { 56, 92, 38, 97, 90, 89 }

              index_value = arr_example . index_value( 3 )   // It searches index value 3 i.e, 97

Insertion Operation

The insertion operation in an array data structure is used to add new elements at a specified position within the array. This operation may involve shifting existing elements to create space for the new element, depending on the position where the insertion takes place.

Example : arr_example [6] = { 56, 92, 38, 97, 90, 89 }

arr_example ( 2, 80 ) // It inserts 80 in index number 2 .

Deletion Operation

A deletion operation is used to remove elements from a particular index of an array.

Example :  arr_example  [6] = { 56, 92, 38, 97, 90, 89 }

arr_example . remove (90) // delete (remove) an element.

Traversing

In traversing we are accessing each element from an array to display.

Example : arr_example  [6] = { 56, 92, 38, 97, 90, 89 }

                  for arr_element in arr_example

                  print arr_element  //  printing an element from arr_example

Sorting Operation

   In data structures, sorting an array means arranging its elements in a specific sequence, such as in ascending order (lowest to highest) or descending order (highest to lowest).

Example :  arr_example [6] = { 56, 92, 38, 97, 90, 89 }

                 arr_example.sort ( reverse = true )

Complexity Analysis in Array Data Structure

Analyzing complexity of an array in data structures is an approach that defines the difficulty of a problem via space and time complexity. It is a very important concept in algorithms to execute any program because it compares the algorithm by different input sizes. Time complexity differs when we perform different operations in an array.

Here is a table below that represents the time complexity of multiple operations performed on an array.

Operations	Time Complexity
Access	O (1)
Linear Searching	O (n)
Binary Searching	O (log n)
Insertion of an element at the end	O (1)
Insertion of element in the middle	O (n)
Deletion of an element at the end	O (1)
Traversal	O (n)

The space complexity of an array is O ( p ) where ‘p’ represents the size of the array.

Complexity analysis is an important approach for both experienced and beginner so that they will optimize their code and understand the algorithm for better performance.

Complexity analysis of an array depends upon the type of operation performed in an array along with whether the array is static or dynamic.

Advantages of Array Data Structure

Easy Implementation 

Implementation of arrays in data structure is easy as compared to other data structures like linked lists, queues , stacks etc. It is very easy for beginners to understand such easy implementation and structure flow.

Static Size ( Fixed Size of an Array)

Static size of an array is an advantage as compared to the dynamic structures because it reduces overhead and possible memory fragmentation.

Flexibility of Supporting Data Types

Arrays support multiple data types to store elements as it increases flexibility and is considered to be an application.

Faster Data Access

Due to the consecutive storage location of storing data in an array , accessing of elements from the array becomes faster so it becomes cache friendly and improves performance.

Disadvantages of Array Data Structures

Insertion & Deletion Cost

Adding or removing elements in an array is time consuming as it increases cost during insertion and deletion operation.

Built-in Methods

Arrays does not have advanced built-in methods for performing searching or insertion operations as compared to advanced data structures like ArrayList in Java programming language.

Conclusion

In this article we have discussed the most important topics that help to understand the basics and complexity analysis of an array in data structure. 

Along with examples it becomes very easy for beginners in data structures to understand the actual definition and basics of an array. By understanding arrays in data structures  programmers can easily solve a wide range of computational problems  and optimize solutions for better performance.