
1.Two types of tea, A and B, are mixed and then sold at Rs. 40 per kg. The profit is 10% if A and B are mixed in the ratio 3 : 2, and 5% if this ratio is 2 : 3. The cost prices, per kg, of A and B are in the ratio
=> Let the per per kg price of both A and B type of tea is x and y. When mixed in 3:2, the profit becomes 10% at 40rs/kg. So Cp is =40/1.1=400/11
Similarly when mixed in 2:3 the profit is 5% so CP =40/1.05=800/21

So 3x+2y=400/11
And 2x+3y=800/21
Now solving the two equation we will get the ratio but it will take more than 2 min so there is other way to formulate the ratio in less time.
Divide the 1st equation by y and 2nd by x. We get
3(x/y)+2=400/11y
And 2+3(y/x)=800/21x
Taking x/y=k
(3k+2)/(2+(3/k))=(400/11y)/(800/21x)=21k/22
From this we can get the value of k=19/24.
2.If among 200 students, 105 like pizza and 134 like burger, then the number of students who like only burger can possibly be
=> Let the number of students like both the burger and pizza is x and y is the number students like none

So 200=105+134-x+y
Or,x=39+y
Number of students like only burger =134-x=134-(39+y)=95-y
To evaluate the range of number of students like only burger we can minimize the vlaue of y.
Y can be 0 thus the upper range of number of students like only burger becomes=95-0=95.
Also y can he Maximum=200-134=66
So lower range of number of students like only burger =95-66=29.
So the range is from 29 to 95.
Only 93 lie in that rigion.
3. A tank is fitted with pipes, some filling it and the rest draining it. All filling pipes fill at the same rate, and all draining pipes drain at the same rate. The empty tank gets completely filled in 6 hours when 6 filling and 5 draining pipes are on, but this time becomes 60 hours when 5 filling and 6 draining pipes are on. In how many hours will the empty tank get completely filled when one draining and two filling pipes are on?
=> Let x be the fraction of the tank filled by the inlet pipe in 1 hr y be the fraction of the tank emptied by the outlet pipe in 1 hr.

So, 6x-5y=⅙ as the tank is filled in 6 hr as from the 1st case.
Similarly 5x-6y=1/60 as in 2nd case the tank was filled in 60 hr.
We get 2 equation and from this we get x=1/12 and y=1/15
Now from the question 2x-y=2*1/12-1/15=⅙-1/15
=5-2/30=3/30=1/10
So the tank will be filled in 10 hr with 2 inlet and 1 outlet pipe.
4. log12 81=p then 3(4-p)/(4+p) is equals to
=> P= log12 81 =log12 3^4 =4 log12 3
3(4-p)/(4+p)

=3(4-4 log12 3)/(4+4 log12 3)
=3(1-log12 3)/(1+log12 3)
=3(log12 12 – log12 3)/(log12 12+log12 3)
=3(log12 12/3)/(log12 12*3)
=3(log12 4)/(log12 36)
=Log12 4^3/log12 36
=Log12 64/log12 36
=Log12 8²/log12 6²
=Log12 8/ log12 6
=Log6 8
5. A CAT aspirant appears for a certain number of tests. His average score increases by 1 if the first 10 tests are not considered, and decreases by 1 if the last 10 tests are not considered. If his average scores for the first 10 and the last 10 tests are 20 and 30, respectively, then the total number of tests taken by him is
=> This question of is very logical and it Will be difficult if we take variables and all, first catch is average increases and decrease by 1, this is the crux. Assume total test are n, when average increases by 1 then we can say 10A-(sum of first 10) will be equal to n-10. The moment you understand this it will be cakewalk. To make more clarity let’s move back to basic average theorem, if all the no before Average are removed then whatever value they will left will be equally divided in the remaining no and since average is increasing so it means we are removing no before A( not necessarily all). Same case with the decrease so here (sum of last 10) – 10A will be equal to n-10. That’s all, from above equation sum of first10 + sum of last10) =20A and that’s we now 200+300 =20A, A=25 so average =25. When first 10 removed average of T11 toTN =26 and when last 10 removed then Average of T1 to T(n-10)= 24. Make this in sum form ie T11 to Tn=26(n-10) and sum of T1 to T(n-10)=24(n-10),when we will subtract this T11 toT(n-10) which is common in both will get canceled. We will get 300-200=2(n-10), 50=n-10,n=60.

Another solution
=> Let S is the sum.
X is the number of students and a is the average
S/x=a
Considering all tests
(S-200)/(x-10)=a+1… excluding first 10 tests
(S-300)/(x-10)=a-1.excluding last 10 tests
S=ax..eq1
S=190+ax-10a+x..eq2
S=310+ax-10a-x..eq3
10a-x=190..by putting 1 in 2
10a+x=310..by putting 1 in 3
Adding both
20a=500
a=25
X=60
6. In an apartment complex, the number of people aged 51 years and above is 30 and there are at most 39 people whose ages are below 51 years. The average age of all the people in the apartment complex is 38 years. What is the largest possible average age, in years, of the people whose ages are below 51 years?

=> There are 30 people age above 51 and atmost 39 below 51.
Overall average is 38., So total age of both above and below 51 is =(30+39)*38=69*38=2622
Now we have to maximize the average age people below 51 so we have to take minimize the average age of above 51.
Minimum average of people above 51 is 51.
So total age of above 51=51*30=1530
So total age of below 51 =2622-1530=1092
Average=1092/39=28
7. If x is a positive quantity such that 2^x = 3^log5 2 , then x is equal to

=> 2^x=3^log5 2
Or, log5 2^x=log5 3^log5 2
Or,xlog5 2=log5 2* log5 3
Or,x=log5 3
Or,x=1+log5 3-1
=1+log5 3- log5 5
=1+ log5 (⅗)
8. Given an equilateral triangle T1 with side 24 cm, a second triangle T2 is formed by joining the midpoints of the sides of T1. Then a third triangle T3 is formed by joining the midpoints of the sides of T2. If this process of forming triangles is continued, the sum of the areas, in sq cm, of infinitely many such triangles T1, T2, T3,… will be,
=> Sides of Equilateral triangle formed by joining the mid points of a equilateral triangle will be half of the side of outer equilateral triangle
area = rt3/4 ( 24^2 + 12^2 ……)
24^2 + 12^2 …..
infinite Gp with common ratio = ¼

Sum = 24^2/ ¾
Sum = 768
area = rt3 * 768 /4
area = 192rt3
9. A trader sells 10 litres of a mixture of paints A and B, where the amount of B in the mixture does not exceed that of A. The cost of paint A per litre is Rs. 8 more than that of paint B. If the trader sells the entire mixture for Rs. 264 and makes a profit of 10%, then the highest possible cost of paint B, in Rs. per litre, is
=> Let the quantity of paint A is A and so as for B.Also A
has to be greater than B. So maximum value B is 5.
Thus A+B =10 now let the CP of B is x and price of A is

X+8.
Now A*(x+8)+Bx=264/1.1=240
Or, Ax+A8+Bx=240
Or,x(A+B)+8A=240
Or,10x+8A=240
Or,10x+8(10-B)=240
Or,10x-8B=160
Or,10x=160+8B
Or,5x=80+4B
Maximum of B is 5
So x=100/5=20
So the highest possible cost of B =x=20.
10. A right circular cone, of height 12 ft, stands on its base which has diameter 8 ft. The tip of the cone is cut off with a plane which is parallel to the base and 9 ft from the base. With π = 22/7, the volume, in cubic ft, of the remaining part of the cone is

=> Height of cone that is extracted from larger cone is 3 . Using similarity diameter is 2
volume of frustum is pi*h*(R^2 + r^2 + R*r)/3
R = 4 and r = 1 . h = 9
So volume is 198
11. If f(x+2) = f(x) + f(x+1) for all positive integers x, and f(11) = 91, f(15) = 617, then f(10) equals.

=>f(15) = f(13) + f(14)
f(15) = f(11) + f(12) + f(13) + f(12)
f(15) = f(11) + f(10) + f(11) + f(12) + f(11) + f(10) + f(11)
f(15) = 5(f(11)) + 3(f(10))
617 – 455 = 3(f(10))
162 = 3(f(10))
54 = f(10)
12. Raju and Lalitha originally had marbles in the ratio 4:9. Then Lalitha gave some of her marbles to Raju. As a result, the ratio of the number of marbles with Raju to that with Lalitha became 5:6. What fraction of her original number of marbles was given by Lalitha to Raju?
=> R/L = 4/9

R = 4L/9
R+x/ L-x = 5/6
6R + 6x = 5L – 5X
11x = 5L – 6R
11x = 5L – 24L/9
11x = 21L/9
33x = 7
X = 7/33
13. John borrowed Rs. 2,10,000 from a bank at an interest rate of 10% per annum, compounded annually. The loan was repaid in two equal instalments, the first after one year and the second after another year. The first instalment was interest of one year plus part of the principal amount, while the second was the rest of the principal amount plus due interest thereon. Then each instalment, in Rs., is
=> 2.1 lakhs * 1.1 = 2.31

If he pays x amount
(2.31 – x)* 1.1 = x
2.31*1.1 = 2.1x
X = 1.21 Lakhs
14- In a circle, two parallel chords on the same side of a diameter have lengths 4 cm and 6 cm. If the distance between these chords is 1 cm, then the radius of the circle, in cm, is
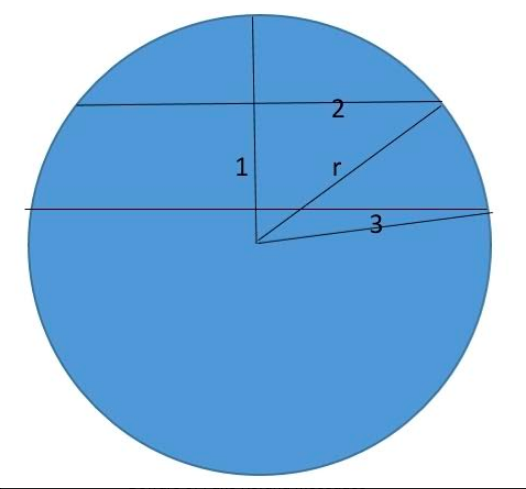
=> Let r be the radius
And ,x be the distance of the middle point of the nearest cord from the centre.

So,
X^2 + 9 = r^2
(x+1)^2 + 4 = r^2
X^2 + 9 = (x+1)^2 + 4
X^2 + 9 = x^2 + 1 + 2x + 4
X = 2
So r = rt13
15. Humans and robots can both perform a job but at different efficiencies. Fifteen humans and five robots working together take thirty days to finish the job, whereas five humans and fifteen robots working together take sixty days to finish it. How many days will fifteen humans working together (without any robot) take to finish it?
=>human = H
robot = R
(15H + 5R )30 = 60(5H + 15R)

15H + 5R = 10H + 30R
5H = 25R
H = 5R
So 16H can do work in 30 days
Total work = 480
H = 1
so 480/15 = 32 days
16. Given that x^2018y^2017 = 1/2 and x^2016y^2019 = 8, the value of x^2 + y^3 is
=> (X^2018*y^2017)/(x^2016*y^2019)=(½)/8
Or,x²/y²=1/16
Or,x²=y²/16
X²+y³=y²/16+y³=y²/16(1+16y)
The answer would be in the form 1+16y
Only possible option is 33
Taking 1+16y=33or, y=2
Putting it we get = 2²/16(1+16*2=4/16*33=33/4
17. In an examination, the maximum possible score is N while the pass mark is 45% of N. A candidate obtains 36 marks, but falls short of the pass mark by 68%. Which one of the following is then correct?
=> Let the passing mark is x.

So x*(1-0.68)=36
Or,x*.34=36
Or,x=36/.34=225/2
Let the maximum mark is y
So,y*0.45=225/2
Or,y=250
Option d is the answer.
18. A wholesaler bought walnuts and peanuts, the price of walnut per kg being thrice that of peanut per kg. He then sold 8 kg of peanuts at a profit of 10% and 16 kg of walnuts at a profit of 20% to a shopkeeper. However, the shopkeeper lost 5 kg of walnuts and 3 kg of peanuts in transit. He then mixed the remaining nuts and sold the mixture at Rs. 166 per kg, thus making an overall profit of 25%. At what price, in Rs. per kg, did the wholesaler buy the walnuts?
=> Let the per kg CP of peanuts =10x.

So the per kg CP of walnuts =30x.
Now price at which the shopkeeper buy 8kg of peanuts =10x*8*1.1=88x.(1.1 multiplied for 10% profit)
Similarly price at which the shopkeeper buy 16kg of walnuts is =30x*16*1.2=576x.
Total cost to shopkeeper=664x.
Now the shopkeeper lost 3kg of peanut and 5kg of walnuts.
The mixed the remaining. Remaining total=5+11=16 kg.
Total price of 16kg of mixture=16*166 which is 125% of 664x.
So 664x*1.25=16*166
Or,x=3.2
So price of walnut=30x=30*3.2=96.
19- Let ABCD be a rectangle inscribed in a circle of radius 13 cm. Which one of the following pairs can represent, in cm, the possible length and breadth of ABCD?

=> Diagonal of the rectangle = Diameter of the circle.
Assuming the the centre of the rectangle and the circle is the same point.
Let the length and breadth of the rectangle is x,y.
Now the ∆ABD which is a right angle triangle has the height as x and base as y, so x²+y²=(hypotenuse)²=(2*13)²=26²
Now going through options only 24 and 10 satisfy the condition.
20. How many numbers with two or more digits can be formed with the digits 1,2,3,4,5,6,7,8,9, so that in every such number, each digit is used at most once and the digits appear in the ascending order?

=> The numbers are 1,2,3,4,5,6,7,8,9
We have to made numbers of 2 or more digits using this numbers.
Total 2 digit numbers = 9c2
Total 3 digit numbers= 9c3
Total 9 digit number 9c9=1
Total= 9c2+9c3+….+9c9
=(9c0+9c1+9c2+….+9c9)-(9c0+9c1)
=2^9-(1+9)
=512-10
=502
21- Let f(x) = min{2×2,52−5x}, where x is any positive real number. Then the maximum possible value of f(x) is

=> F(x)=min(2x²,52-5x)
As x is real the minimum will be when 2x²=52-5x
Or,2x²+5x-52=0
Or,(2x+13)(x-4)=0
Or,x=-13/2 and 4
Putting both the value we get 32 at x=4 as the minimum number.
22. The number of integers x such that 0.25 < 2^x < 200, and 2^x +2 is perfectly divisible by either 3 or 4, is
=>
x = {0,1,2,3,4,5,6,7}
2^x = {1,2,4,8,16,32,64,128}
2^x + 2 = {3,4,6,10,18,34,66,130}
so numbers divisible by 3 or 4 are 5

23. In a circle with center O and radius 1 cm, an arc AB makes an angle 60 degrees at O. Let R be the region bounded by the radii OA, OB and the arc AB. If C and D are two points on OA and OB, respectively, such that OC = OD and the area of triangle OCD is half that of R, then the length of OC, in cm, is

=> Radius =1 cm.
Area of the 60° arc =(60/360)*π*r²
=π*1²/10
=π/10
Now the point on OA as C and point on OB as D, Such that OC=OD and the angle between them is 60°. So, The triangle OCD is equilateral triangle.
Also, Area of the triangle OCD = Half the area of arc=π/20
Let the side of the triangle as x
So √3/4 *x²=π/20
Or,x²=√(π/4√3)
24. Point P lies between points A and B such that the length of BP is thrice that of AP. Car 1 starts from A and moves towards B. Simultaneously, car 2 starts from B and moves towards A. Car 2 reaches P one hour after car 1 reaches P. If the speed of car 2 is half that of car 1, then the time, in minutes, taken by car 1 in reaching P from A is

=> Let the total distance =4x
So AP=x and BP=3x.
Let car 1 take t hr to reach p so car 2 take (t+1) hr to reach p.
Speed of car 1=x/t and car 2=3x/(t+1)
According to the problem
X/t=2*3x/(t+1)
Or,x=5xt
Or,5t=1
Or,t=⅕ hr
25.If u^2 + (u−2v−1)^2 = −4v(u + v), then what is the value of u + 3v?
=> u²+(u-2v-1)²=-4v(u+v) .

By opening the equation we will get
2u²-2u+8v²+4v+1=0
Or,2(u²-2*u*½+¼)+8(v²+2*v*¼+1/16)+1-½-½=0
Or,2(u-½)²+8(v+¼)²=0
We know that when a²+b²=0
Then a² and b² both have to be individually equal to 0.
So, from there we get u=½ and v=-¼.
Putting that in u+3v we get the overall value as -¼.
26. If log2(5 + log3 a) = 3 and log5(4a + 12 + log2 b) = 3, then a + b is equal to
=> Log2 (5+log3 a)=3

Or,5+log3 a =2^3=8
Or,log3 a=8-5=3
Or,a=3^3=27
Log5 (4a+12+log2 b)=3
Or,4a+12+log2 b=5^3=125
Or,4*27+12+log2 b=125
Or,log2 b =125-120
Or,log2 b=5
Or,b=2^5=32
So a+b=32+27=59
27. In a parallelogram ABCD of area 72 sq cm, the sides CD and AD have lengths 9 cm and 16 cm, respectively. Let P be a point on CD such that AP is perpendicular to CD. Then the area, in sq cm, of triangle APD is
Area of parallelogram = a * b * sin(theta)
72 = 9*16* sin(theta)
sin(theta) = ½

Theta = 30 degrees
Now APD is a right angle triangle with angle ratio 30 : 60 : 90
so side ratio will be 1:rt3 : 2
8 : 8rt3 : 16
so area is ½ * b*h = ½ * 8*8rt3 = 32rt3
28. Let x, y, z be three positive real numbers in a geometric progression such that x < y < z. If 5x, 16y, and 12z are in an arithmetic progression then the common ratio of the geometric progression is
=> X,y,z are in geometric progress such that x<y<x.
Let x=a/r y=a and z=ar

So 5x=5a/r 16y=16a 12z=12ar
Now 5x,16y and 12z are in Arithmetic progress. So, 2*16a=5a/r+12ar
Or,32ar=5a+12ar²
Or,32r=5+12r²
Or,12r²-32r+5=0
Now going through options, Option b only satisfying the equation.
29. Train T leaves station X for station Y at 3 pm. Train S, traveling at three quarters of the speed of T, leaves Y for X at 4 pm. The two trains pass each other at a station Z, where the distance between X and Z is three-fifths of that between X and Y. How many hours does train T take for its journey from X to Y?

=> Let the speed of train T is 4x and thus speed of train S is 3x. At 4 pm or in 1 hr the train T will travel 4x distance and reached a point support A.
Now from A to Y both train started at 4 pm and meet at z. So Speed ratio of that train is 4:3 so Distance ration would also be 4:3.
So Az:yz=4:3
From the question we also say that XZ:YZ=3:2
Comparing both the ratio we get XA:AZ:ZY=1:8:6.
Train T travel XA in 1 hr so it will take 1+8+6=15 hr to reach Y from X.
30. A right circular cone, of height 12 ft, stands on its base which has diameter 8 ft. The tip of the cone is cut off with a plane which is parallel to the base and 9 ft from the base. With π = 22/7, the volume, in cubic ft, of the remaining part of the cone is
=> Radius=4 ft and height=12.

When parallely cutted along the base the small cone has height 3 and radius let say x.
Now by compairing 2 triangles of these 2 cones we get 12/4=3/x
Or,x=1
Area of the remaining portion
=⅓ πr1²h1-1/3πr2²h2
=1/3π{4²*12-1²*3}
=1/3π*189
=⅓*22/7*189
=198.
31. When they work alone, B needs 25% more time to finish a job than A does. They two finish the job in 13 days in the following manner: A works alone till half the job is done, then A and B work together for four days, and finally B works alone to complete the remaining 5% of the job. In how many days can B alone finish the entire job?
=> B take 25% more time than A.
So time takes ratio=4:5.

As time taken is inversely proportional to efficiency.
Thus efficiency ratio=5:4
Now 50% work was done by A and 5% by B so 45% was done by both A and B in 4 days .
As there efficiency ratio=5:4 so A did 25% if the work in 4 days, or 100% in 16 days and B did 20% of the work in 4 days or 100% in 20 days.
One can do this question without using the 13 data.
So 13 is redundant here.
32. Points E, F, G, H lie on the sides AB, BC, CD, and DA, respectively, of a square ABCD.If EFGH is also a square whose area is 62.5% of that of ABCD and CG is longer than EB, then the ratio of length of EB to that of CG is
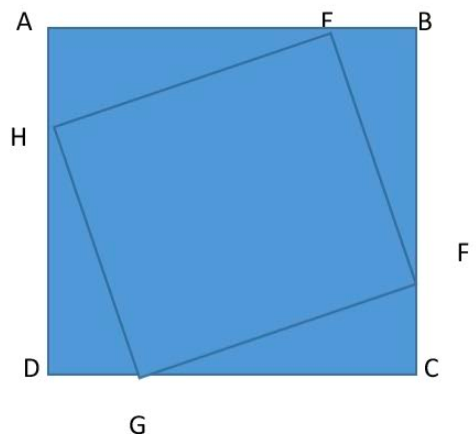
=> Let AE = 1
AH = k

HE = rt(k^2 + 1 )
Area of small square = k^2 +1
Area of larger square = (k+1)^2
(k+1)^2 * 62.5/100 = k^2 + 1
(K^2 + 1 + 2k ) * 5 = (k^2 + 1 ) * 8
5K^2 + 5 + 10k = 8K^2 + 8
0 = 3K^2 – 10k + 3
0 = 3k^2 -9k – 1k + 3
0 = 3k(k – 3) -1 (k-3)
0 = (3k-1)(k-3)
K = 1/3 or 3/1
33. Each of 74 students in a class studies at least one of the three subjects H, E and P. Ten students study all three subjects, while twenty study H and E, but not P. Every student who studies P also studies H or E or both. If the number of students studying H equals that studying E, then the number of students studying H is
Exactly 3 = 10

Only H and E = 20
Only P = 0
As number of students in H = E
74 – 30 = 44
44/2 = 22
So students in H = 22 + 30 = 52
34. While multiplying three real numbers, Ashok took one of the numbers as 73 instead of 37. As a result, the product went up by 720. Then the minimum possible value of the sum of squares of the other two numbers is

=> Let the other two numbers are x,y
So 73xy-37xy=36 xy which is equal to 720
Or,xy=20
As x and y both are real so taking x=y
X²=20
Or,x=y=√20
Now x²+y²=20+20=40

