Now since only 8 months are left for CAT 2025, the strategic preparation not only needs syllabus coverage but rigorous practice, and mastering the art of solving CAT-level questions. Applying the learnt concepts to different questions not only boosts ones confidence but also evaluates the preparedness for exam. In CAT 2024 we have more than 500+ 99 percentilers and after a detailed analysis of their CAT prep journey one thing we found out in common was that all of these students were a part of iQuanta’s special batch – IIM ABC batch. Until last year we started this batch in the month of August but seeing the success ratio and to break our own record this year iQuanta’s IIM ABC batch will start in the month of April itself. This batch will have two phases. In phase 1 the question will be from easy to moderate level and then we will move to advanced level questions. Here are some of the questions from the IIM ABC Batch.
So if you are a CAT 2025 aspirant aiming to score 99+ percentile then join this Whatsapp Group to be a part of this special batch getting launched soon!
Join Whatsapp Group Here!

Why Choose iQuanta’s IIM ABC Batch?
- Majority CAT Toppers Were From this Legendary Batch:
- In CAT 2024, more than 500 students were from iQuanta and most of them were from this IIM ABC Batch.
- They all were thankful for being a part of this batch as the CAT level questions were really helpful.
- Early Start for Maximum Impact:
- Unlike previous years, when this batch used to start in August, this year it will begin in April, and will have two phase. The first phase will have easy to moderate CAT level questions.
- Early preparation ensures ample time for concept clarity, practice, and mock test analysis.
- IIM ABC Batch Will Have Two-Phase Learning Approach:
- Phase 1: Focus will be on easy-to-moderate level questions to build a strong foundation.
- Phase 2: Shift to advanced-level questions, ensuring you’re ready for even for the toughest questions that you can get in the exam.
- Comprehensive Practice Material in IIM ABC Batch With More Than 8500 CAT Level Questions:
- The IIM ABC batch includes topic-wise assignments, daily practice sessions, and you will get access to over 8,500+ CAT-level practice questions.
- With iQuanta’s unique dual teaching method, you’ll not only understand the core concepts but also learn to apply those concepts to CAT level questions.
- Instant Doubt Solving:
- Be it day or night, iQuanta’s team is always available 24/7 to resolve your doubts within minutes.
Q. P = 54n – 32n, where n is an even natural number and is not a multiple of 4. Which of the following does not divide P?
A. 317
B. 13
C. 11
D. 7
Solution:
1. We can use the following rules:
If n is odd (an + bn) is divisible by (a + b) and
If n is even/odd, (an – bn) is divisible by (a – b)
Now HCF (n, 4) = 2, where n is an even number.
So, 54n – 32n= 58k – 34k , where k is odd
58k + 34k = (58)k – (34)k, where k is odd.
The remaining term of the expansion of (58k – 34k) will be divisible by (58 – 34 )
(58k – 34k) = (54 – 32) (54 + 32) A, where A is constant
or, (58k – 34k) = (52 – 3) (52 + 3) (54 + 32) A
= 22 x 28 x 634 x A
This is divisible by 7, 11, and 317 but not by 13.
Q. John has a deck of 52 uniquely numbered cards from 1 to 52. He draws two cards one after the other, without putting the first card back into the deck. What is the probability that the first card John draws is card number 1, and the second card he draws is card number 13?
A. 12652
B. 12704
C. 12601
D. 12650
Solution:
2. Drawing without replacement means that once the first card is picked up, it gets discarded. Now, the pool for the second card gets reduced by one card i.e., it becomes 51 instead of 52.
One card can be picked from 52 ways i.e., n(S) = 52.
There is only one, 1 numbered card in the pack. Hence it can be picked only in one way i.e., n(A) =1
∴ P (the first card is 1 numbered) = 152
Since the cards are drawn without replacement, there are now 51 cards left. Hence n(S) = 51
Again, there are only 13 number of cards i.e., n(B) = 1
∴ P (second card is 13 numbered) = 151
Hence, Required probability = 152151=12652
Hence option A is the correct answer.
So if you are a CAT 2025 aspirant aiming to score 99+ percentile then join this Whatsapp Group to be a part of this special batch getting launched soon!
Join Whatsapp Group Here!

Q. The heat radiated by a certain machine per unit of time varies directly with the cube root of the excess temperature of 37 C. The heat radiated by the machine per second is 27 joules when the temperature inside the machine is 64 C. Find the temperature (in C) inside the machine when the heat radiated by the machine per second is 63 joules.
Solution:
3. Let’s assume that the heat radiated by the machine per unit of time = H
According to question, heat (H) at certain temperature of T C.
H T-3713
=> H = k T-3713
At T = 64 C, given that H = 27
=> 27 = k 64-3713 = k * 3
=> K = 9 ——–(1)
Now, we need to find T, when H = 63 joules
=> H = kT-3713
=> 63 = kT-3713 —–(2)
Put the value of k = 9 in (2), we get
=> 7 = T-3713
=> 343 = (T – 37)
=> T = 380 C
Hence 380 is the correct answer.
Q. In a sports team 70% of the players are children and x% of the children and y% of the adults are newcomers. The total number of newcomers who are children and adults who are seasoned players equals the total number of seasoned players who are children and newcomers who are adults. Which of the following could be the set of values of (x, y)?
A. (50, 30)
B. (40, 30)
C. (45, 30)
D. (35, 15)
Solution:
4. Let the total number of players be T
Children = 0.7T and Adult = 0.3T
New players who are children = x100×0.7T
New players who are adults = y100×0.3T
ATQ,
x100×0.7T+100-y100×0.3T=100-x100×0.7T+y100×0.3T
=> 7x + 3(100-y) = 7(100-x) + 3y
=> 14x – 6y = 400
=> 7x – 3y= 200
From the given options, only option D satisfies the answer i.e., x = 35 and y = 15
Hence option D is the correct answer.
Q. If p1p2 + 1 is a perfect square where p1 and p2 are the prime numbers picked from the first 120 natural numbers, then how many pairs of (p1, p2) satisfy this?
A. 20
B. 12
C. 16
D. 8
Solution:
5. p1p2 + 1 = Perfect Square
p1p2 + 1 = k2
k2 – 1 = p1p2
p1 and p2 are prime numbers which exist at a gap of 2.
So, possibility that (p1 , p2) satisfy are –
(3, 5), (5, 7), (11, 13), (17,19), (29,31), (41,43), (59,61), (71,73), (101,103), (107,109)
Hence total 10 values are possible.
But, p1 and p2 are defined variables so, we have to count it as two distinct cases
Hence, total 10 * 2 = 20 values are possible.
So if you are a CAT 2025 aspirant aiming to score 99+ percentile then join this Whatsapp Group to be a part of this special batch getting launched soon!

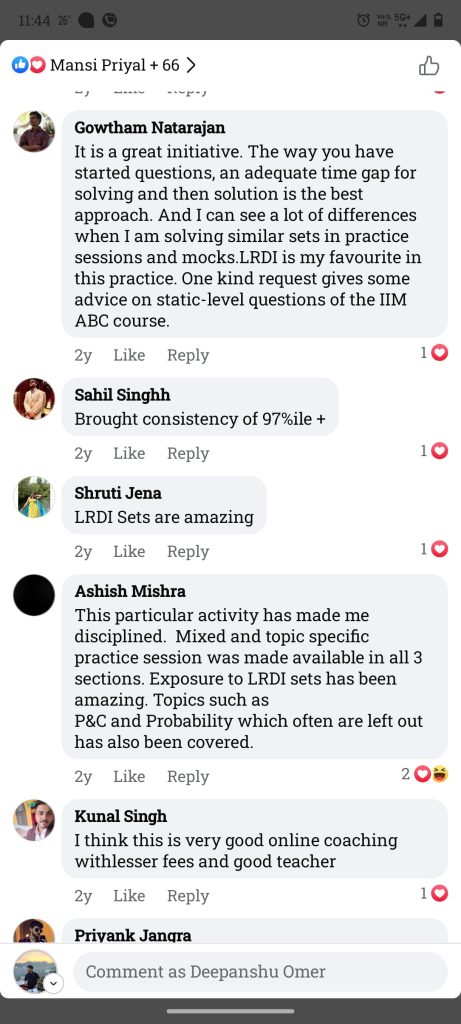
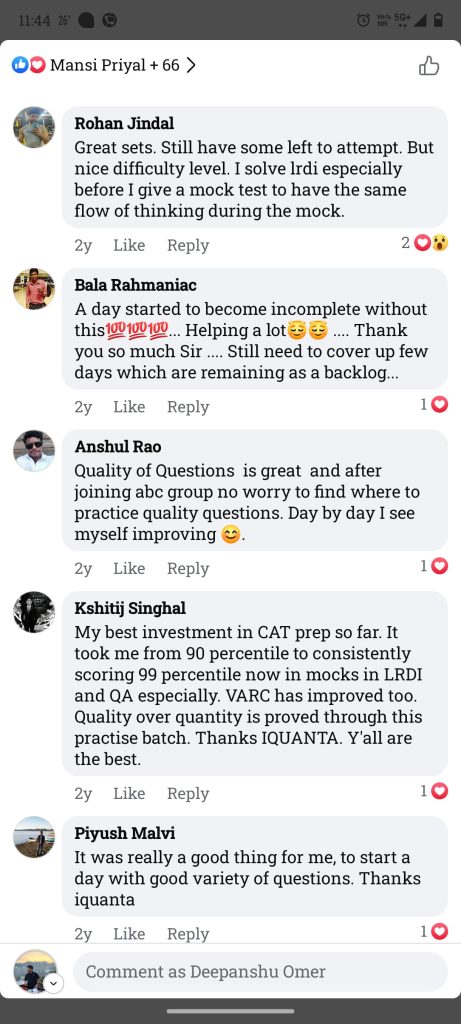
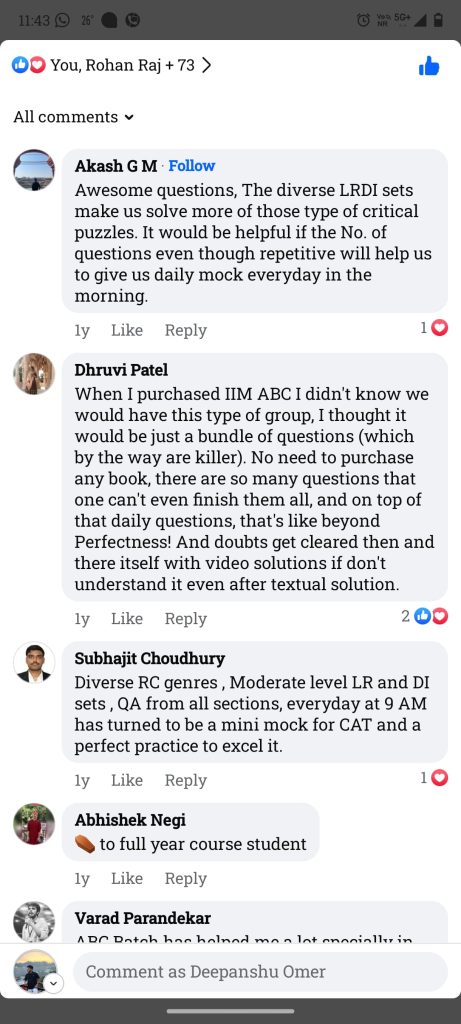
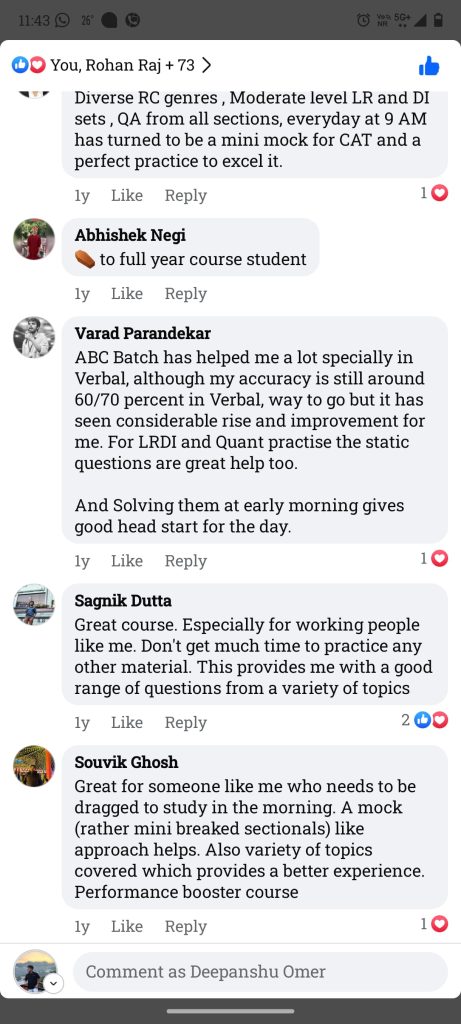
Check out the IIM ABC Feedback Shared by Our Students
Join the Largest CAT Preparation Community in India


