Graphs are the most important and versatile concept in computer science. There are many real world applications that simulate graph data structure which includes the friends recommendation of facebook, google maps shortest path finding application and many more.
Unlike trees, graphs use network models and are a non-linear data structures. A graph is a network model that organizes data when we want to show how things are connected or solve problems where connections between the objects are crucial.
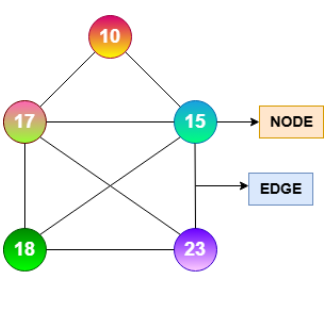
In this blog we will be covering the introduction of graph data structure, types of graph data structure , graph representation in data structure, graph traversal algorithms in data structure like BFS ( Breadth First Search ) and DFS ( Depth First Search ) along with different real life application of graph data structure.
What is Graph Data Structure?
Graph is a data structure and it is used to represent the relationships between the entities. Graph data structure contains nodes and to connect nodes between each other we have edges. In the given diagram nodes are the individual entities or points within the graph data structure.
Graph data structure is really powerful because they bring clarity to complexity by reducing intricate systems into a simple structure of nodes and edges. This allows us to visualize and analyze relationships in a comprehensive yet intuitive way. Their adaptability makes them even more valuable, as the same graph structure can represent vastly different systems, such as transportation networks, supply chains, or social interactions. Moreover, graphs are fundamental in problem-solving, offering solutions to challenges like finding the shortest path in navigation apps, detecting clusters within social groups, or analyzing influence within a network. This combination of simplicity, flexibility, and utility makes graphs an indispensable tool in understanding and addressing real-world problems.
If we are taking real life examples of social media platforms like Facebook and Instagram, they are highly using graph data structures. We are the users on social media platforms representing nodes of a graph and edges representing some kind of relationship between the users.
Types of Graph Data Structure
Directed Graph
Directed graph in graph data structure represents the direction between the nodes. The edges connected between the nodes show a specific direction that relates the relationship between the nodes in one way. So this graph represents the relationship flow between nodes in one direction but not necessarily in the reverse direction as well.
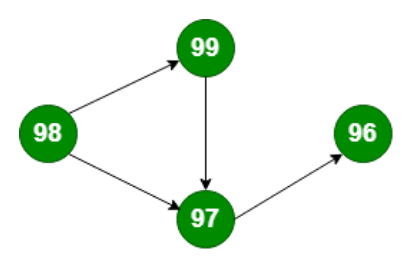
Undirected Graph
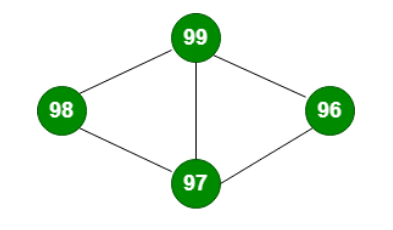
Undirected graph is said to be just the opposite of a directed graph in which the relationship flow between the nodes is bidirectional. Let’s consider two nodes in the below diagram i.e, 99 and 97 , you can move from 99 to 97 and also from 97 to 99 without any restriction.
Weighted Graph
Weighted graph is an important graph that represents the numerical value at every edge considered as weights. These weights on the edges represent the cost, distance, time, capacity or any other measures related to the relationships between the nodes.
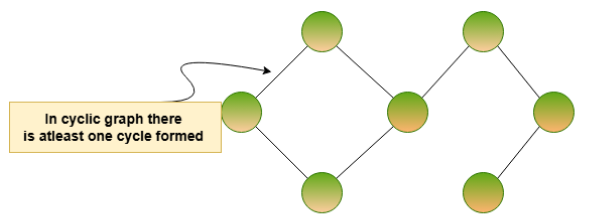
Cyclic Graph
Cyclic graph contains one cycle in its concept. A cycle happens when you can start at a node, follow edges, and come back to the same node without reusing any edge or node along the way.
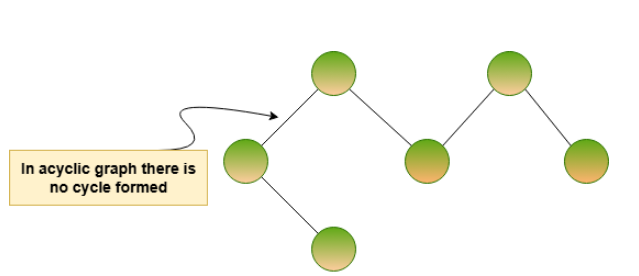
Acyclic Graph
Acyclic graph is just the opposite of a cyclic graph and has no cycle.. This means there are no paths in the graph that start and end at the same node while passing through other nodes or edges. As this is just the opposite of a cyclic graph.
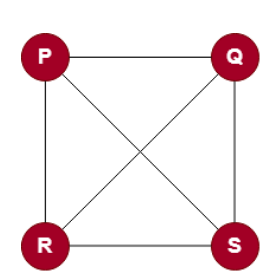
Complete Graph
A complete graph is a graph where every node is directly connected through the edges as there are no missing edges between any two nodes. It is a highly connected graph where every node is connected to every other node.
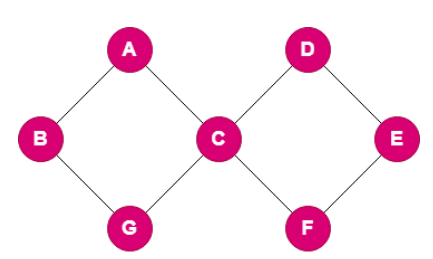
Connected Graph
A connected graph connects every possible node to others, which means you can visit from any node to any other node by following the possible edges presents in the graph.
Disconnected Graph
A disconnected graph is exactly the reverse ( opposite ) of the connected graph present in the graph data structure. In a simple way, this graph has one or more separate components that have no edges connecting them.
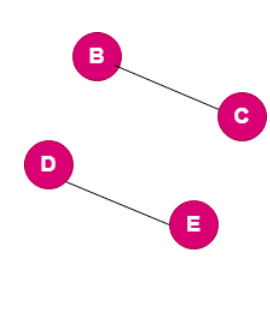
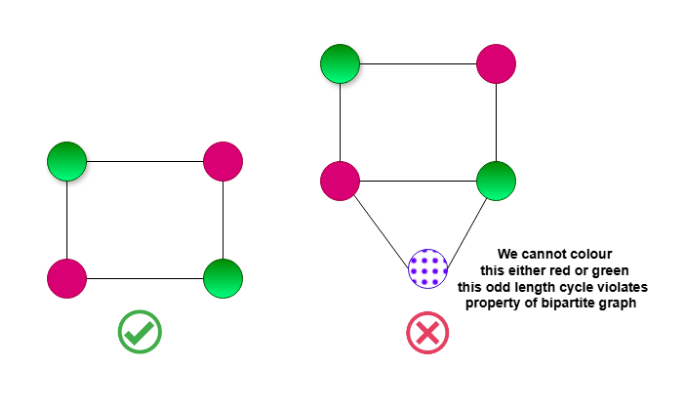
Bipartite Graph
A bipartite graph is a type of graph that can be split into two nodes (groups) and all the connections (edges) in the graph only go between these two groups, never within the same group.
Planar Graph
In real life applications there are a lot of uses of planar graphs that includes circuit designing, network planning etc. Planar graphs can be easily represented on a plane surface and edges are not crossing with each other for the concept of planar graph.
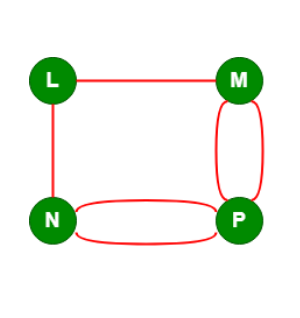
Multigraph in Data Structure
A multigraph is a graph data structure that allows multiple connections between the same pair of nodes, and it can also have loops. This makes it more flexible for modeling real-life systems with repeated connections or pathways.
Eulerian Graph Data Structure
Imagine you are walking along the paths (edges) in a neighborhood and you want to visit every path exactly once and return to where you started. If it’s possible, the graph is an Eulerian graph.
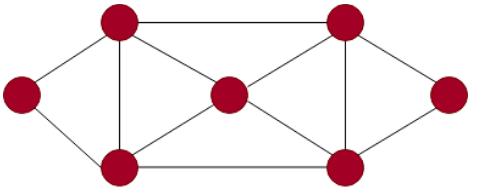
Hamiltonian Graph in Data Structure
Imagine you’re planning a trip to visit all the cities in a region without visiting any city more than once and then returning back to your starting city. If this route is possible, the graph is called a Hamiltonian graph.
Graph Representation in Data Structure
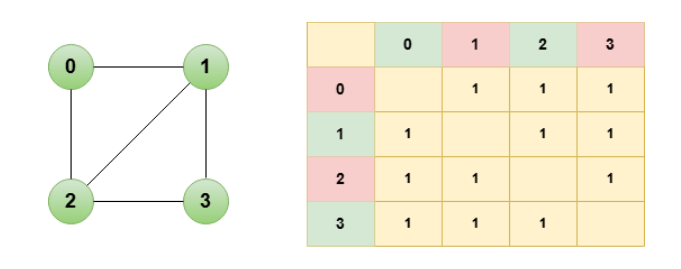
Adjacency Matrix
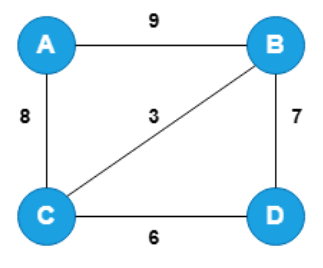
Graphs in data structures represented in a two possible manner through the adjacency matrix and adjacency list . Adjacency matrix is basically a square matrix that represents the entire graph in the form of a table or matrix . The table represents the entry of the edges between the respective nodes in the graph.
This is the best and easiest way to understand the representation of graphs in data structure. In the example given below we have 4 nodes in the graph and the table represents the entry of ‘1’ if that particular edge exists between the nodes otherwise the blank box.
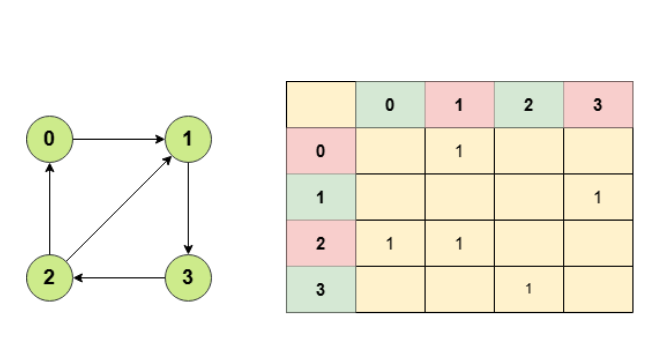
Adjacency List
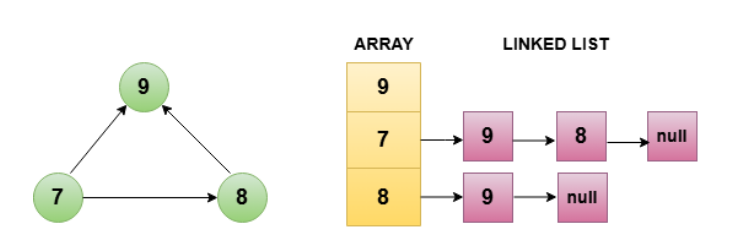
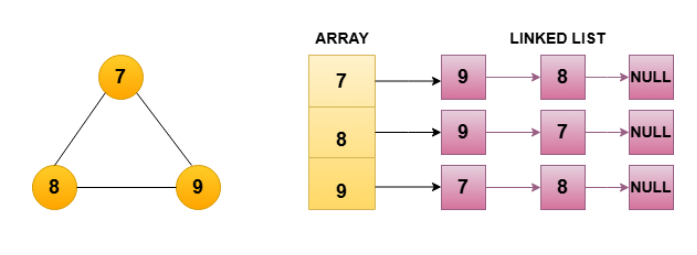
Adjacency list is another way to represent the graph data structure. In an adjacency list, each node (vertex) has its own list that contains all the nodes (vertices) it is connected to. Instead of using a 2D matrix (like in adjacency matrix representation), the adjacency list uses a list of lists (or a dictionary) to store edges. In the given below diagrams you can visit for both undirected or directed graph representations as adjacency list.
Graph Traversal in Data Structure
Breadth First Search Graph Traversal Algorithm
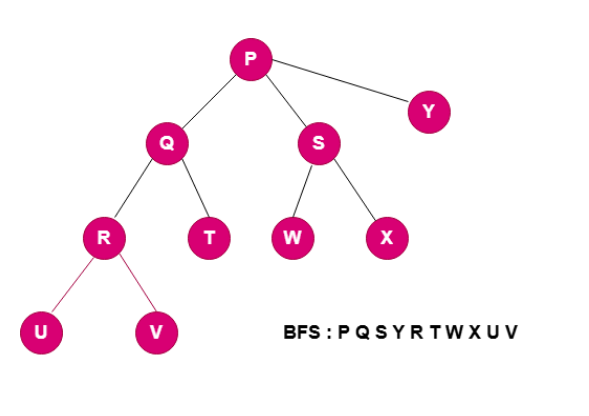
Breadth-First search is an important algorithm for graph traversal. This algorithm visits all nodes in the graph but layer by layer ( you can understand level by level). First , it visits all neighbours of the particular level or layer and then visits the next level.
Here is the algorithm :
Step 1 : Insert the start node in the queue and mark that as visited.
Step 2 : while the queue is not empty:
Dequeue a node and process it.
Step 3 : Enqueue all its unvisited neighbors and mark them as visited.
Step 4 : Repeat until queue is empty
Depth First Search Graph Traversal Algorithm
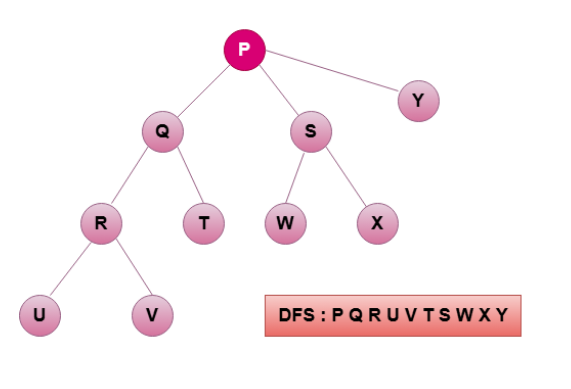
Depth First Search algorithm is an important concept for graph traversal. This Algorithm visits every node in the graph but the way it visits is little different in comparison to breadth first search algorithm. DFS visits every node as far as possible for every branch of a graph before backtracking.
Here is the algorithm :
Step 1 : Start from the given node
Step 2 : Mark the started node as visited
Step 3 : Recursively explore each unvisited neighbor of the current node.
Step 4 : Once all the neighbors visited the current node then backtrack.
Step 5 : Repeat these steps again and again until each and every node of a graph mark as visited.
Application of Graph in Data Structure
Social Media Platforms
On social media platforms we users represent the nodes of a graph data structure and the followers and following represent the edges. Graphs on social media platforms connect followers and build connections between friends along with suggestions.
Graphs in Machine learning
Graph data structure is used in machine learning to perform various tasks like community detection with the help of graph neural networks. They are basically used to predict tasks and build relationships between data points.
Graphs in Computer Networks
Graphs have wide applications in computer networks to maintain the flow of data and efficiency. Devices like routers and switches represented as nodes and the flow of data representing the edges that manages the topology of the network.






![Top 10 Applications of Linked List Data Structure [2025]](https://www.iquanta.in/blog/wp-content/uploads/2025/02/WhatsApp-Image-2025-02-01-at-2.48.42-PM-218x150.jpeg)

