Queue is a fast and flexible data structure in the computer science domain. Remember we are standing in a line and purchasing tickets , the person who comes first serves first in that situation.

In the similar manner queue works on the principle of FCFS ( First Come First Serve ) and in different books you got to know this term by the FIFO ( First In First Out ) concept. 

Among the diverse data structures, queues stand out for their simplicity and practicality because the queue follows FIFO structure ( the first element in the queue will serve first ) .

This functionality of queues makes them fast and flexible in managing and storing data.

In this blog, we will cover the introduction of queue in data structure, types of queue, circular and priority queue, complexity analysis of queue, all basic operations performed in queue data structure along with their applications.

What is the Queue in Data Structure ?

Queue is a fundamental concept of managing and storing data in the data structure ( linear data structure ).

Queue is opened from both the end that makes it flexible and fast for inserting and deleting elements in data structure .

There are different terminologies that we are using in queue to understand its representation : 

• Enqueue ( Insertion operation in queue ) 

Enqueue operation of queue inserts elements in a queue. Insertion of elements in the queue done from the rear end.

• Dequeue ( Deletion operation in queue ) 

Deletion operation of the queue removes elements from the queue. Deletion will be done from the front end of the queue.

The representation of the queue looks like the arrangement of elements in the list where both the ends are opened. Pictorial representation of the queue in data structure depicted below :  

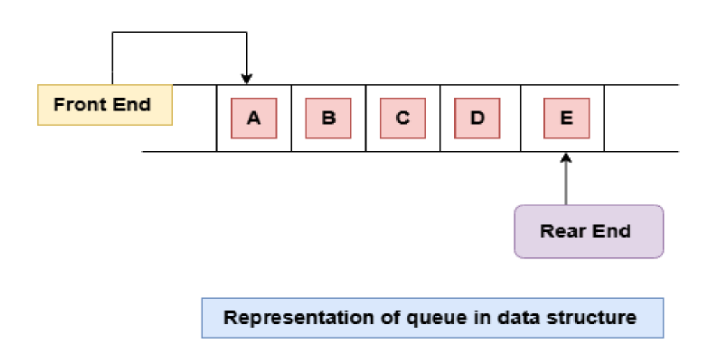
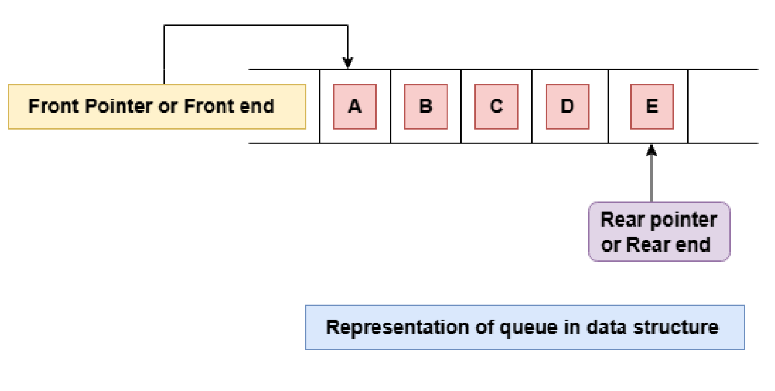
There are some cases when we are performing deletion and insertion in a queue . We have to consider two pointers in the queue i.e, front pointer and rear pointer.

Case 1 : If queue is empty ( there is no element in queue ) 

Front > Rear  or Front = Rear = -1 

Case 2 : If queue is not empty ( there is at least one element in the queue )

Front < Rear 

Case 3 : If there is only one element in the queue 

Front = Rear

Case 4 : For enqueue operation 

Rear =  Rear + 1

Types of Queue in Data Structure 

There are different types of queue we are using in data structure for managing and storing data efficiently.

Linear Queue Data Structure

This Queue is simply behaving like a simple queue data structure where elements can be accessed sequentially through the indices positions. 

Linear Queue maintains the FIFO order ( First In First Out )  to simply manage elements in the queue.

If we are using a fixed size array in a linear queue then memory management is quite complicated as we have lost a lot of memory( vacated ). 

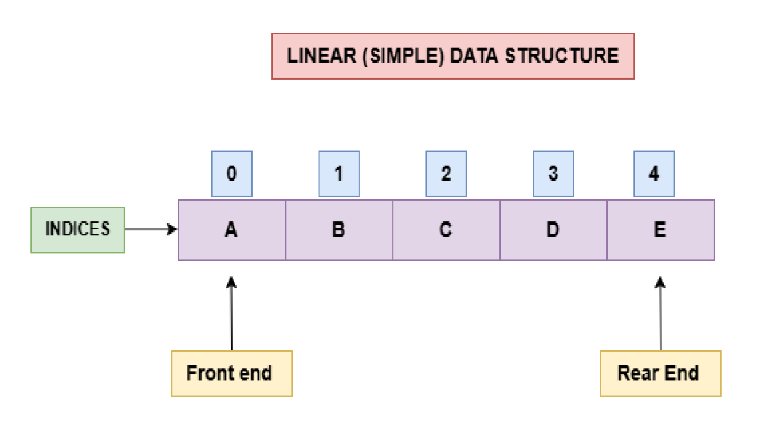
Here, we have two ends: front end and rear end in the simple queue data structure. Insertion of elements performed at the rear end and deletion of elements performed at the front end in the FIFO order. If the memory is full in the linear queue then overflow condition occurs.

Circular Queue Data Structure ( Circular Workflow )

Circular queue works in a circular workflow in a queue data structure, its first element connected to the last element and more memory efficient in comparison to the linear data structure.

In the circular queue data structure we are wrapping the elements around. In a circular queue data structure if we are inserting an element and due to space if it is required to wrap around our element to the front end then we can do it. 

If overflow condition occurs in a circular queue data structure then there is no space left to wrap up the spaces.

Here is the pictorial representation of using circular queue data structure for better understanding of the concept : 

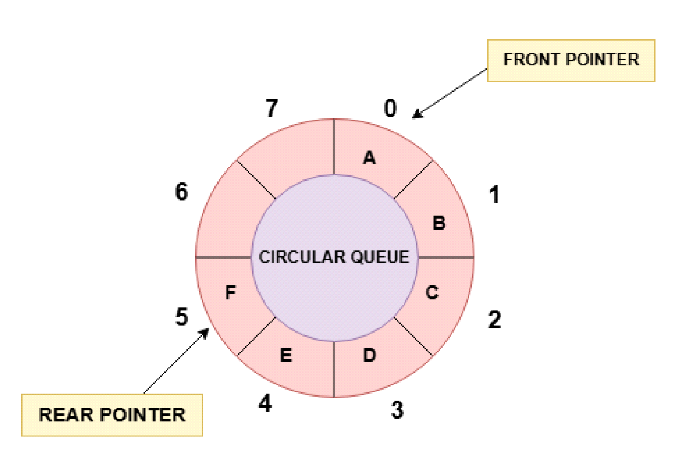
Note : In Circular queue modulo operation required for the rear and front end operations whereas in linear ( simple ) queue data structure start and end represented by the indices ( positions ) of the sequentially arranged list (fixed array ) in a queue data structure.

Therefore,  Rear =(  Rear + 1 ) % size of array.

Priority Queue Data Structure

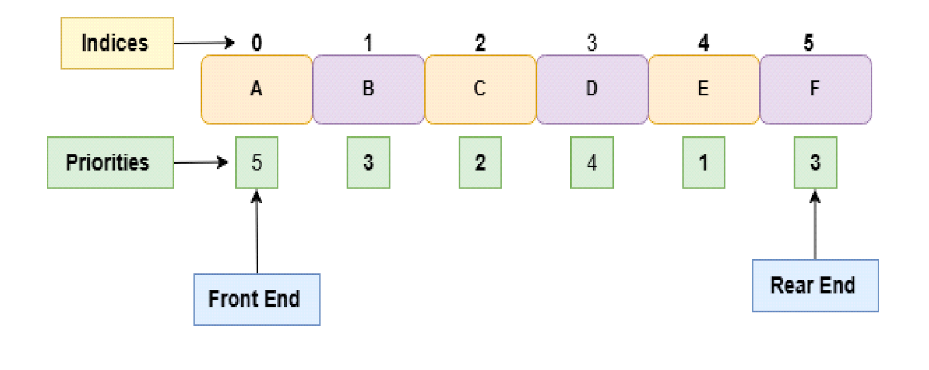
This data structure is a special version where arrangement of elements are according to their priority values. Each element has their own priority value, same or different associated with it accordingly.

We can implement priority queues with different data structures like linked lists , arrays as well as heap data structure ( min- heap and max- heap data structure ) .

If we want to dequeue ( remove an element ) from the priority queue data structure then we have to remove the element first with the highest priority associated with it and then remove the element with the lowest priority ( priority of elements in a priority queue decides according to the situation ).

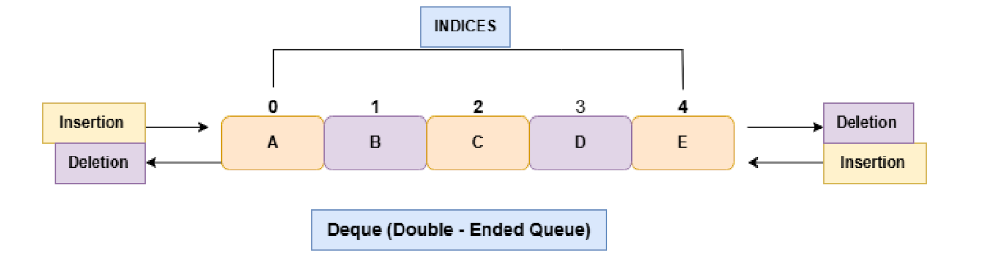
Deque Data Structure( Double – Ended Queue )

Deque is a special type and advanced version of the queue . This queue allows both insertion and deletion operations from both the ends of the queue data structure.

The deque data structure is more flexible and fast in comparison to the linear and priority queue data structure.

If we want to push elements at the front or from the back in the deque data structure we generally do it in O ( 1 ) time complexity.

If we have to pop the elements from both the ends we generally do it in O ( 1 ) complexity  which is really good in terms of optimizing the code structure.

Below is the pictorial representation of the deque data structure that helps you to understand how the operations in deque actually performed.

Queue Operations in Data Structure

There are basic operations we have performed in a queue data structures:

Enqueue Operation ( Inserting an element ) in queue

Enqueue operation is a basic operation to perform on elements when we have to insert ( elements ) in the queue data structure.

Generally we add elements in the queue from the rear end using the rear pointer.

Peek Operation

Peek operations resembles the basic pop and push operation in the stacks and queues.

With the help of pop ( ) operation we will return the element from the front of the queue list without actually removing the element from the queue.

Dequeue operation

Dequeue operation in queue used to perform the deletion operation ( remove an element from the queue) .

Generally we are removing the elements from the queue using the front pointer from the front end. 

Is Full ( ) operation ( To check whether the queue is full or not )

This operation is performed in the queue to check whether the given function checks with the elements in a queue to find whether the given queue is full or empty for  the given situation. 

Is Null ( ) operation ( To check whether the queue is Null or not )

This operation is performed in the queue to check whether the given function checks with the elements in a queue to find whether the given queue is Null or not for the given situation. 

Complexity Analysis of Queue

According to the different operations we have performed in the queue data structure of various versions we have time complexities of each operation mentioned in the table listed below :

Types of Queues	Enqueue operation	Dequeue operation	Peek ( ) operation	Space Complexity
Deque(Double – Ended Queue)	O ( 1 )	O ( 1 )	O ( 1 )	O ( n )
Priority Queue	O ( log n  )	O ( log n  )	O ( 1 )	O ( n )
Circular Queue	O ( 1 )	O ( 1 )	O ( 1 )	O ( n )

Application of Queue Data Structure

Process scheduling and process management in operating systems

Process scheduling in the operating system is done on the basis of FCFS ( First Come First Serve ) approach . Operating systems manage different queues like Job queue, ready queue , device queues etc  for efficiently performing their process management.

Network traffic management in computer networks

Routers and switches generally use queues to manage the data in the form of packets ( networking term of data used in network layer ) before forwarding to the next available device.

Customer service domain

In a customer service domain calls are placed in a queue until you find the next agent in a process. Customers in a customer service are arranged in the FIFO ( First In First Out ) workflow the way they arrive in the system.