Trees are a fundamental data structure widely used in computer science and programming. They provide an efficient way to store, retrieve, and organize data, enabling various applications in different domains. In this article, you will learn about the applications of tree in data structures and how it can be used to solve many problems.
Tree data structures are hierarchical models of data with the parent-child data structure. They occupy a crucial position in a great number of computing science applications because of their appropriateness for the representation of intricate relationships between the data, searching and sorting capabilities, and dynamic data processing.
What is a Tree Data Structure?
A tree is a type of data structure that represents a hierarchical relationship between data elements, called nodes. A node at the top of the tree is called the root and the elements coming below the root node are called the child node.
Any given child node could have one or more child nodes of their own and the structure created such as branches.
The nodes that do not have a child node that is directly under the node are known as terminal nodes or sometimes as the leaf nodes.
This tree structure is often used to represent hierarchical relationships, such as file systems, company organizational charts, and family trees.
Applications of Tree in Data Structures
File Systems
One of the most common applications of tree in data structures is in organizing file systems.
These systems have always been highly rigid structures in terms of hierarchy, and directories and subdirectories are nodes in the tree.
The root node, a field of two bytes, is the first directory while each subdirectory of it is a child node. Files in particular are best stored as the leaves of the tree where they connect to the associated directories.
Trees remain one of the most effective ways of moving around file systems because they allow users to quickly and easily find their files.
In addition, copying, moving, renaming, and removing files, as well as creating new directories are very efficient processes that make them a critical part of contemporary computing.
Database Indexing
Trees have an important role in the database systems but their usage is significant while indexing which is important whenever fast data access is required. Trees such as the B-trees and B+ trees are used to maintain efficiency and the vast database systems deal with them constantly.
- B-Trees: These self-balancing trees divide data into the set of blocks stored in nodes thus minimizing the no of disk accesses during the searching operation. Every node contains several keys and this makes the searching and replacing easier and faster.
- B+ Trees: More closely related to B-trees, these types of trees contain all real information in the leaf nodes. These leaves are implemented as linked lists so that the sequential access for range searching of the range queries is faster. For these reasons, B+ trees are particularly appropriate for databases in which sorted data access and fast search are needed.
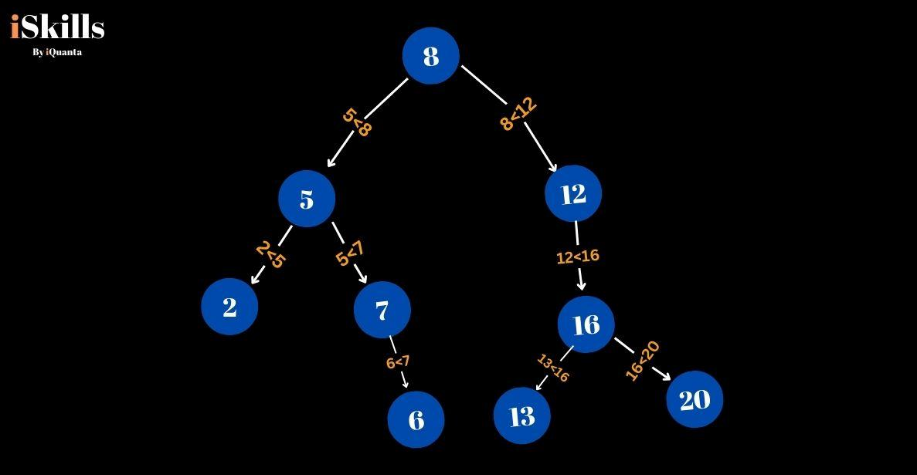
Binary search tree ( BST )
Binary Search Trees (BST) are hierarchical data structures designed for efficient operations on ordered datasets used in various applications. They sort data in such a way that each node holds a single value with all the lesser values on the left and all the greater values on the right. They say that this arrangement helps one to make speedy searches, insertions, and deletions since the number of comparisons made is low.
The search process implies the move down from the root node left if the target value is smaller than the current node value right if it is greater.
This process is repeated until the value is retrieved or a node that contains only one copy of the said value is encountered. Balanced BSTs remain efficient throughout a system while unbalanced BSTs may reduce a system’s efficiency to linear memory search.
AVL Trees
AVL trees use a form of self-balancing for binary trees that is achieved without additional insertion or deletion operations. They are beneficial mostly in cases where the tree goes through many changes and other operations are to stay fast.
These trees work by maintaining the height difference, (also known as the balance factor) between the left and right subtrees. When this difference goes beyond the normalized values, rotations are executed to bring the counts back. This mechanism ensures that AVL trees are always optimized for large and dynamic data as required by most applications today.
Decision Trees
Decision trees are a kind of tree data structure for use in a variety of machine learning computations to make yes or no decisions during a selection process that is given a set of guidelines or standard rules.
Instead, they function through partitioning the data into nodes based on certain criteria. Here, every node is a decision point and every edge is an outcome that is available to the decision-maker at that point. They help this structure simplify the decision on what action needs to be taken based on the available information.
Trie Trees
Trie trees is one of the applications of tree in data structures. A trie tree is a data-retrieving tree structure used for storing strings and searching characters in a string. They are particularly easy to implement in cases where there is a propagate-in word search or prefix query, like the auto-complete procedure or spell check.
The node is a character of a string in the words being searched and edges depict the relation of these characters. These strings are built up by moving along those edges from node to node. Such a structure enables fast accessing of strings and prefixes to be used more frequently in text processing than other structures.
Huffman Trees
Huffman trees are a kind of binary tree that is implemented when compressing data. They operate by deciding on how to allocate variable length codes to characters in a string such that strings with frequent characters receive short code strings. This makes it possible to squash the data while at the same time keeping all the information intact.
Specifically, Huffman trees utilize a binary tree through the characters in the string. A set of more frequencies has short codes assigned to it while a set with fewer frequencies has longer codes assigned. This ensures that the compressed data set is smaller as much as it possibly can be and yet still contains all the info.
Applications of Huffman Trees:
- File Compression: As previously mentioned, Huffman coding finds application in compression algorithms including ZIP, GZIP, and RAR while minimizing data size.
- Multimedia Compression: Huffman trees are also used in the image or video formats, JPEG and MP4 respectively to compress such files by an even smaller size while maintaining their quality.
Segment Trees
Segment trees are special kinds of tree-based structures that can be used to carry out range search operations on large datasets. They are especially useful for such uses as trying to find either the maximum or value in a range of numbers.
Segment trees work by using segments to store information where segment data in the segment tree is what is actually involved. All elements of the tree are segments and all the lines between the elements are linkages of those segments. This formation of data will permit a quick search of particular information within a particular range of the data set.
Applications of Segment Trees
- Range Queries: Segment trees are typically used in problems from competitive programming and data processing when it is necessary to update some range of an array and then request the sum of elements in this range or find the minimal/ maximal units at the range of indices.
- Geospatial Data: In computational geometry, the application of segment trees is in range search problems like sorting the intersection of multiple intervals.
Red-Black Trees
A Red-Black Tree is a self-organizing binary search tree in which every node is tagged with a Red or Black color, to guarantee the tree is balanced upon operations such as insertion and deletion.
Applications of Red-Black Trees:
- Memory Management: The uses of Red-Black trees In an operating system are to facilitate efficient dynamic memory allocations.
- Routing Algorithms: Red-Black trees find applications in network routing protocols including OSPF for handling routing tables with the aim of providing a fast path for data packets.
KD-Trees in Nearest Neighbor Search
KD-Trees work like binary trees in that they strive to sort points from a k-dimensional space. This is especially useful where applications of multidimensional data are in use.
Applications of KD-Trees:
- Machine Learning: KD-Trees are great for the k-Nearest Neighbor (KNN) algorithms where points must be classified depending on their proximity to other randomly located points in the high-dimensional area.
- Computer Vision: KD-Trees are used in computer graphics for keeping fast collision detection and ray casting, which enhances the results of rendering in the 3D graphics software.
Conclusion
In 2024, tree data structures will continue to be a cornerstone of modern computing, providing effective ways of finding, storing, and rearranging information in a short time.
Indeed, starting from binary search trees applied to search data quickly to Huffman trees applied for data producing trees are used in all areas of databases, learning machines, networking, and computer graphics.
Adaptive balancing, minimizing time complexity, and accommodating massive amounts of information extol tree data structures as irreplaceable emblems in developing fast, optimal systems. From memory management to file systems and from search operations to just about anything else, the structures inherent in tree form are a cornerstone of the technology world in the year 2024.



