In the data-driven era of computing and programming , tree data structure plays a vital role for storing and managing data efficiently. We have seen data structures like arrays, stacks that store data in a linear form.
Tree in data structure is the most appropriate to store data in a hierarchical form and considered to be an advanced data structure. Trees play a vital role for managing data in a non-linear form (trees don’t store data in a sequential manner like linear data structure does).
In this blog we will be covering introduction to tree in data structure, how to represent tree in data structure along with its basic terminologies, different operations to be performed, real world applications along with advantages and disadvantages of a tree.
What is tree in data structure ?
Trees are versatile data structures that store data in a hierarchical form. In a tree there are different nodes that are connected through the edges and each node contains data and pointers helps to connect different nodes with each other.
Root Node
Root Node in the tree serves as a topmost node. It is the initial point in the tree to reach all other nodes. All the nodes of the tree data structure are directly or indirectly connected to it and the flow of entire tree decides from the root node itself.
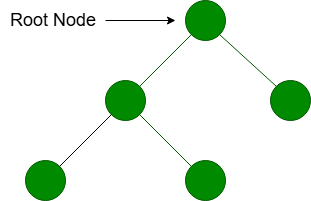
Node
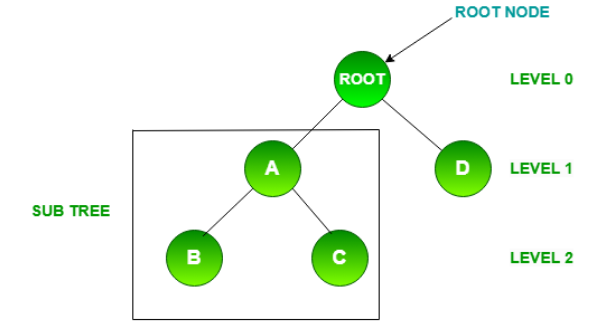
It is a basic terminology which represents data in a tree that are connected with each other through the edges. Node in a tree contains data that we need to store and apart from that A, B, C, D, root all are the nodes given below in the diagram 1.1
Edge
Edge is a connection between two nodes in a tree that joins two nodes together. It’ s main property is to show the relationship between the child node and parent node. It is very important term in a tree to understand relationship between the nodes.
Parent node in tree
A parent node in tree is a node which has one or more child nodes. Example: In the diagram Node A is the parent node of Node B and Node C.
Leaf Node : Leaf nodes in a tree have no child nodes. Example : Node B, Node C, Node D serve as a leaf node in the given diagram.
Height : Height of a tree can be calculated as the longest path from that node to the leaf node.
Height of a tree = Height of a root node.
Depth of a tree : Depth of a tree can be calculated as the number of edges between the root node to the respective node.
Level of a tree : Level of a tree in a data structure can be calculated as the number of connections formed between the root node and the respective node.
Example : Root Node == Level 0 (root node of a tree is at level 0 )
Generations : All the nodes of the same level are considered to be the same generation nodes.
Example : Node A ,Node D == Level 1
Node B, Node C== Level 2
Degree of a node : Degree of a tree can be calculated as the total number of children count of that node.
Degree of a node = Total number of children of a node
Types of trees in data structure
Binary Tree
Binary tree is a most fundamental tree in data structure . This tree has at most 2 children ( i.e 0, 1 ,2 nodes ). It is a foundation for all the specialized trees like AVL tree ( Adelson-Velsky and Landis ) and BST.
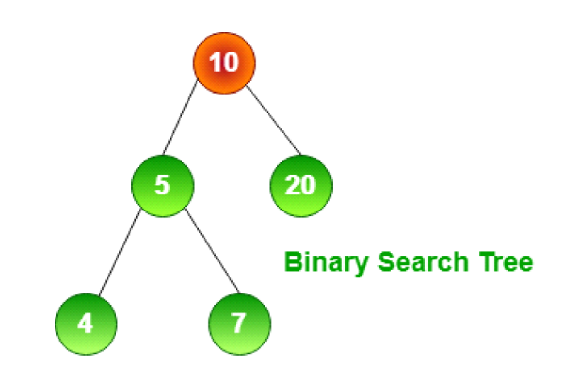
Binary Search Tree (BST)
Binary Search Tree is an important tree for efficient searching, insertion and deletion of a node in a tree.
The Given example below represents the properties of Binary Search Tree (BST) in which node 10 represents the root node of a tree and left child of root node is 5 ( which is lesser than it’s parent node ) and 20 is the right child of the root node ( which is greater than it’s parent node).
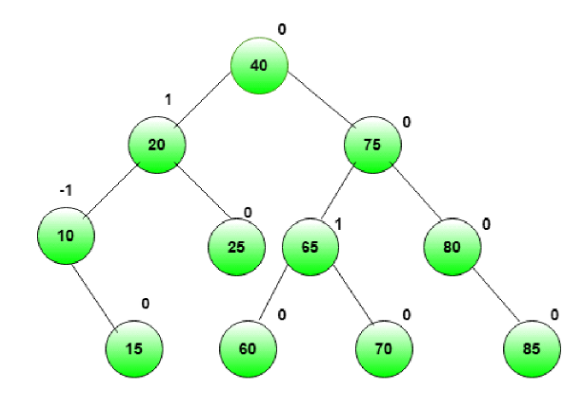
Balanced Binary Tree ( AVL Tree )
Balanced Binary Tree is an extended and more efficient version of binary search tree that improves complexity. The difference in height of the left and right subtree is either -1, 0 ,+1. Rotations will be of four types i.e, LL rotations ( Left Left rotation ) , LR rotation (left right rotation), RL(Right left rotation) rotation, RR (Right Right) rotation.
- AVL trees are the perfect example of the balanced binary search tree as they contain self balancing properties.
- They are used in several computer science fundamentals like file systems for the fast data retrieval.
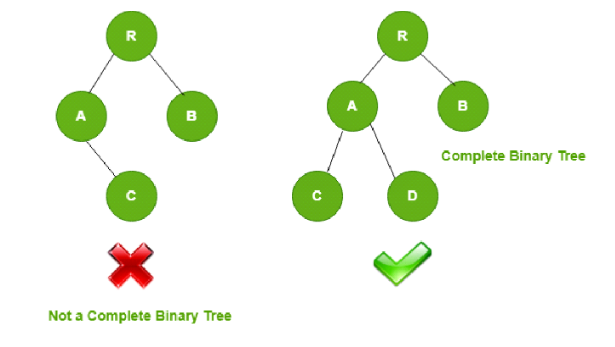
Complete Binary Tree (CBT) in Data Structure
Complete Binary Tree ( CBT ) is another type of tree in data structure in which all the nodes are completely filled till the second last level and in the last level the arrangement of nodes are left aligned ( i.e, the nodes are arranged from left to right ).
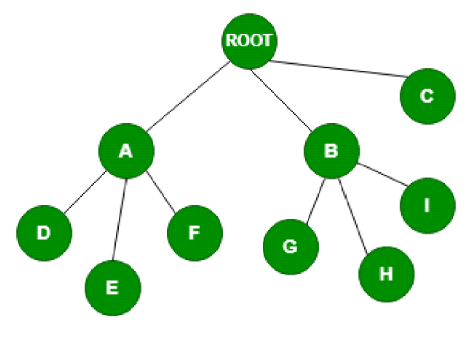
K- Ary Tree in Data Structure
K- Ary tree defines a generalized number of children for each node . Each node in the K-ary tree contains at most k number of children. A full k-ary tree is considered to be full if each node in the tree has 0 or exactly ‘k’ nodes. In the diagram below shown 3- ary tree:
Tree Operations in Data Structure
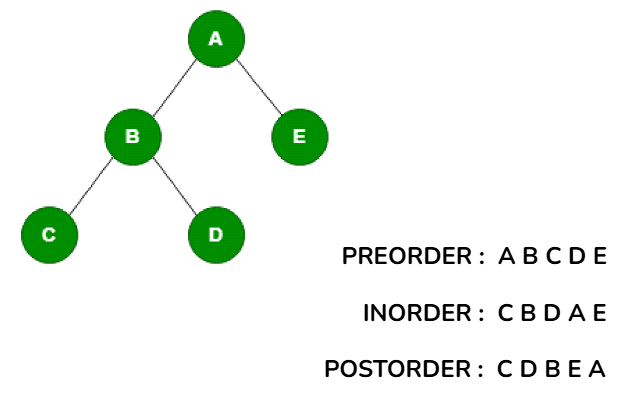
Traversal operation of a tree
Traversal operation in a tree serves as the visiting of each node according to an order. There are different traversals in tree viz. preorder traversal, postorder traversal and inorder traversal.
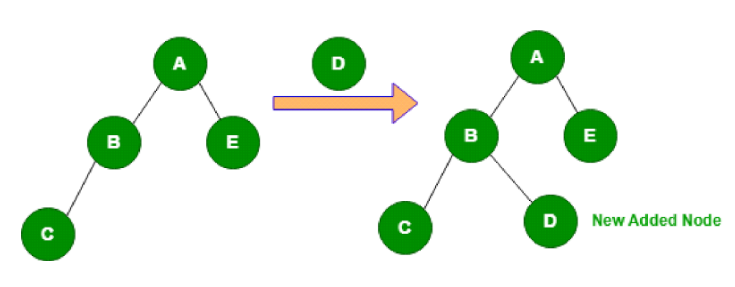
Addition operation of tree in data structure
Addition operation in a tree used for adding a new node in a tree.
In the diagram given below we are actually adding the D node to the tree as the right child of B.
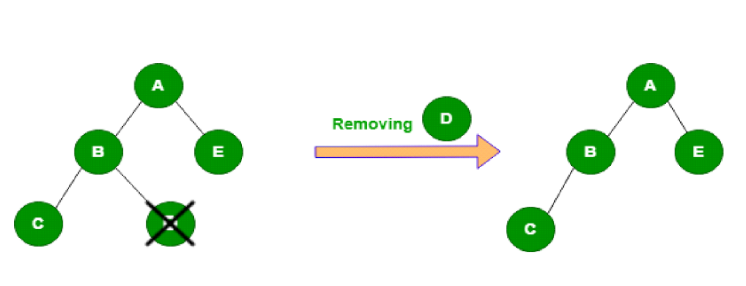
Deletion operation of tree data structure
Deletion operation in a tree data structure is used to delete a particular node from a specified location in a given tree. To practically understand delete operation we have deleted Node D from the tree given in the diagram below.
Search operation of tree in data structure
Search (SEARCHING) operation in a tree data structure searches for a particular node in a tree.
Application of tree in data structure
Networking and routing application
- Tree helps in forming the routing tables to determine the shortest path in a network efficiently.
- Domain Name System uses tree to resolve domain names to IP addresses.
Use of tree data structure in compilers
Compiler is an important and fundamental unit of computer science and it uses AST ( Abstract Syntax Tree ) to represent the structure of source code or proper flow to determine the easy analysis and translations.
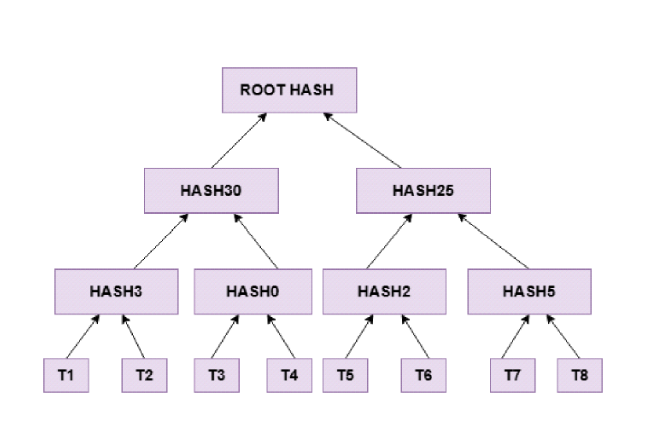
Use of trees in Blockchain
Merkle trees are used in blockchain technology to verify the transactions and security systems. These trees in blockchain and in other security systems are used to minimize the network congestion and enable processes and computation faster.
Advantages and Disadvantages of tree in data structure
Advantages
- Insertion and searching will become more efficient and we will perform these operations in O (log n) time, making them efficient for sorted data.
- Trees provide three different traversal options like preorder, postorder and inorder that helps to traverse the data according to the requirement.
Disadvantages
- Child nodes or pointers in a tree can increase memory usage that cause problems of memory overhead.
- Data ordering no longer remains intrinsic in a tree.
