In the world of computing and programming we have another versatile data structure stack with us. In our day-to-day lives, we encounter many examples that remind us of stacks and how they work, such as a stack of plates. Similarly, we use process scheduling algorithms in operating systems, which involve scheduling processes in system architecture.
Stack is a linear data structure which follows the LIFO structure (Last In First Out) for push (add an element) or pop (delete an element).
In this article we will mainly cover the entire concept of using stack , how we will represent entire elements of using stack in data structure ,various types of stacks in data structures , various operations performed on a stack, analyzing complexity in almost every possible manner, real life examples of using stack data structure and many more.
Let’s dive deep to understand the basic concepts of using stack in data structure .
What is Stack in Data Structure?
Stack is a linear data structure which follows the Last In First Out (LIFO) order to arrange elements. Stack data structure opens from only one end so there is only one possible manner to pop (delete an element) and push (add an element) onto the stack .
In the stack data structure there are different blocks that help you to understand the representation of the stack.
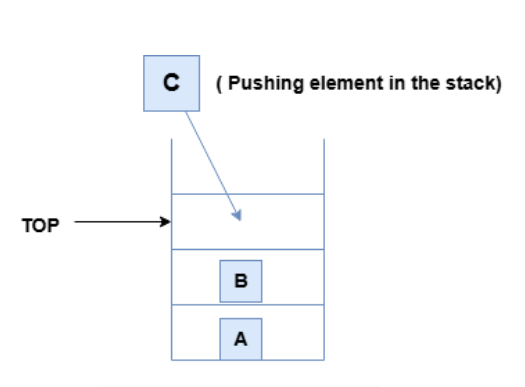
In this pictorial representation above, we are adding element ‘ C ‘ in the stack and a pointer ‘TOP’ pointing to the topmost block of the stack where we need to push an element. Here element ‘ C ‘ added last in the stack.
In stack there are few terminologies that are required to understand the concept of stack in data structure properly :
- TOP : TOP is a pointer in the stack data structure. This pointer in stack points the topmost block of the stack in data structure. If the stack is having the condition of underflow then the value of the TOP is -1 (when stack is empty).
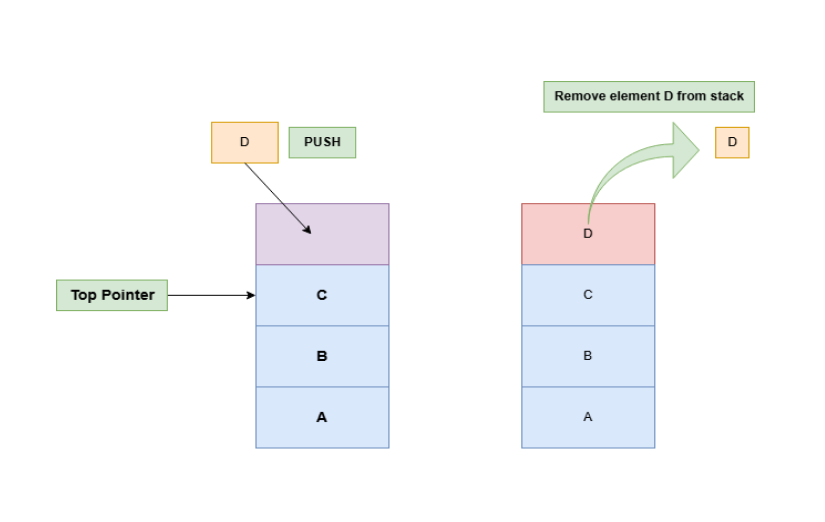
- PUSH (Adding element in the stack) : Push is an operation in the stack , we will add elements in a stack using push( ) operation.
- POP (Remove an element from the stack) : We will remove an element from the stack using the pop ( ) operation.
Types of Stack in Data Structure
Simple Stack
Simple Stacks performs the LIFO (Last In First Out). Push ( ) operation performs to add an element onto stack and pop ( ) operation performs deletion of an element from the top of the stack.
Circular Stack
When we have to work with any cyclic data then we are generally using a circular stack. It is a special version of stack in which the last element of the stack points to the initial element to form a loop or cycle workflow.
Being a developer or programmer it is very necessary to use this efficient stack data structure in competitive coding.
Dynamic Stack
Dynamic stack is more efficient in comparison to simple stack because it grows and shrinks (adjust its size) during execution of the program. It is more memory efficient in comparison to other stack data structures.
Implementation of Stack Data Structure
PUSH( ) Operation
PUSH ( ) operation used to add elements in stack and follows the LIFO operation. Below is the code snippet that helps you to understand how actually push operation works in stack. It is a basic operation have to be performed.
#include <iostream>
#define MAX_STACK 30 // defines the maximum size of the stack
class stack_push {
private:
int arr[MAX_STACK];
int top_pointer;
public:
stack_push(){ // It is a constructor
top_pointer =-1;
}
void push_element(int value){
if (top_pointer>=MAX_STACK-1){
std::cout << "Stack overflow condition";
}
else
{
arr[++top_pointer]=value;
std::cout << value << "push element";
}
}
void show (){
if (top_pointer==-1){
std::cout <<" stack is empty";
}
else{
std::cout << " elements in a stack";
for(int i =0; i<=top_pointer; i++){
std::cout<<arr[i]<< " ";
}
std::cout <<"\n";
}
}
};
int main()
{
stack_push create;
create.push_element(90);
create.push_element(87);
create.show();
return 0;
}
POP( ) Operation
POP( ) operation is used to remove elements from the stack. Below is the code snippet that helps you to understand how actually pop operation works in stack. It is a basic operation have to be performed.
#include <iostream>
#define STACK_SIZE 40 // Define the maximum size of stack
class stack_pop {
private:
int arr[STACK_SIZE];
int top_pointer; // top element of the stack
public:
// we are using constructor here for the initialization
stack_pop() {
top_pointer = -1;
}
// Function to push an element onto the stack
void push_element(int value) {
if (top_pointer >= STACK_SIZE - 1) {
std::cout << "Stack overflow condition occurs";
arr[++top_pointer] = value;
std::cout << value << " pushed onto the stack.\n";
}
}
// Function to pop an element from the stack in data structure
void pop_element() {
if (top_pointer == -1) {
std::cout << "Stack Underflow condition occurs\n";
} else {
std::cout << arr[top_pointer] << " popped from the stack.\n";
top_pointer--;
}
}
// Function to display the current elements in the stack
void show_elements(){
if (top_pointer == -1) {
std::cout << "Stack is empty.\n";
} else {
std::cout << "Stack elements: ";
for (int i = 0; i <= top_pointer; i++) {
std::cout << arr[i] << " ";
}
std::cout << "\n";
}
}
};
int main() {
stack_pop create;
create.push_element(85);
create.push_element(20);
create.push_element(89);
create.show_elements(); // With this function calling we will show all the elements present in the stack
create.pop_element(); // Pop top element
create.pop_element();
create.show_elements(); // showing all the elements after removing
return 0;
}
IsEmpty( ) Operation
IsEmpty( ) operation in a stack is used to check whether the stack consists of elements or not. Below is the code snippet that IsEmpty() function for the stack.
#include <iostream>
#define STACK_SIZE 40 // This macro defines the maximum size of stack
class stack_emptyOps {
private:
int arr[STACK_SIZE]; // Defining array to hold the stack size
int top_pointer; // Points to the top element of the stack
public:
//
stack_emptyOps() {
top_pointer = -1;
}
// function defining here to push an element in the stack
void push_element(int value) {
if (top_pointer >= STACK_SIZE - 1) {
std::cout << "Stack overflow condition occurs here\n";
} else {
arr[++top_pointer] = value;
std::cout << value << " pushed onto the stack.\n";
}
}
// Function defining here to remove(pop) element from the stack
void pop_element() {
if (isEmptyfunc()) {
std::cout << "Stack underflow condition occurs here\n";
} else {
std::cout << arr[top_pointer] << " popped from the stack.\n";
top_pointer--;
}
}
// Function to check if the stack is empty
bool isEmptyfunc() {
return top_pointer == -1; // Returns true if top is -1 (no elements)
}
void show() {
if (isEmptyfunc()) {
std::cout << "Stack is empty.\n";
} else {
std::cout << "Stack elements: ";
for (int i = 0; i <= top_pointer; i++) {
std::cout << arr[i] << " ";
}
std::cout << "\n";
}
}
};
int main() {
stack_emptyOps create;
if (create.isEmptyfunc()) {
std::cout << "The stack is empty.\n";
}
create.push_element(98);
create.push_element(93);
if (!create.isEmptyfunc()) {
std::cout << "The stack is not empty here.\n";
}
create.show(); // show all the stack elements
create.pop_element();
create.pop_element();
create.pop_element();
if (create.isEmptyfunc()) {
std::cout << "The stack is empty again.\n";
}
return 0;
}IsFull( ) operation in stack data structure
The IsFull ( ) operation in a stack is used to check whether the stack has reached its maximum capacity. If the stack is implemented using an array, IsFull ( ) typically compares the current size of the stack to the maximum size of the array. Below is the code snippet where IsFull ( ) operation is used in the stack.
#include <iostream>
#define STACK_SIZE 40 // defining maximum size of the stack here
class stack_full {
private:
int arr[STACK_SIZE];
int top_pointer;
public:
// Constructor to initialize the stack
stack_full() {
top_pointer = -1;
}
// Function defining here to insert element in a stack data structure
void push_element(int value){
if (isfullStack()) {
std::cout << "Stack overflow condition occurs\n";
} else {
arr[++top_pointer] = value;
std::cout << value << " push elements in stack.\n";
}
}
// Function to pop an element from the stack
void pop_element() {
if (isEmptyfunc()) {
std::cout << "Stack underflow condition occurs\n";
} else {
std::cout << arr[top_pointer] << "removing elements from stack.\n";
top_pointer--;
}
}
bool isEmptyfunc() {
return top_pointer == -1; // Returns true if top is -1 (no elements)
}
bool isfullStack() {
return top_pointer == STACK_SIZE - 1;
}
void show() {
if (isEmptyfunc()) {
std::cout << "Stack is empty.\n";
} else {
std::cout << "Stack elements: ";
for (int i = 0; i <= top_pointer; i++) {
std::cout << arr[i] << " ";
}
std::cout << "\n";
}
}
};
int main() {
stack_full create;
if (create.isEmptyfunc()) {
std::cout << "The stack is currently empty.\n";
}
// Pushing elements
for (int i = 1; i <= 3; i++) {
create.push_element(i * 8);
}
create.show();
if (create.isfullStack()) {
std::cout << "The stack is now full.\n";
}
create.push_element(95);
while (create.isEmptyfunc()) {
create.pop_element();
}
if (create.isEmptyfunc()) {
std::cout << “Empty Stack\n";
}
return 0;
}
Analyzing complexity of stack data structure
Analysis of complexity for stack in data structure for any operation in terms of time and space is an important concept to understand to analyze the workflow of an algorithm or while writing the code.
Detailed information of entire operation according to its time complexity is given below where you can cover entire concept at a one place mentioned in the listed table :
| Operations in the stack data structure (Stack operations in data structure) | Time Complexity |
| Push operation in the stack (Adding an element) | O (1) |
| Pop operation in the stack (Remove an element) | O (1) |
| Access operation in the stack | O (n) |
| Search an element operation in the stack (Searching) | O (n) |
Application of stack data structure
Undo / Redo operations in Microsoft word or Photoshop
The stack is used to perform undo and redo operations and stores user actions. In text editors, it facilitates functions like Ctrl+Z (undo) and Ctrl+Y (redo). Whenever the user performs any actions, the stack records these actions. For instance, this functionality is widely used in applications like Microsoft Word and Photoshop.
Memory management in stack
Stack data structure manages the memory allocation for temporary variables. Stack application are also there when we are using local variables in function calls.
Function calls with the help of stacks
Stacks are essential in managing function calls through the call stack, which follows the Last-In-First-Out (LIFO) principle. When a function is called, a stack frame is created and pushed onto the stack. This frame contains important details like the function’s local variables, arguments, and the return address, which is the location in the program where control will return after the function finishes executing. The call stack ensures that the current function’s context is saved before transferring control to the called function.
Browser Navigation (like Google Chrome or Firefox)
Stacks can be used in browser navigation. When a user searches for something or visits a page, the current page URL is pushed onto the stack.
Expression Evaluation and Conversion
Stacks are widely used in evaluating and converting mathematical expressions, such as infix, postfix, and prefix notations. In an infix expression (e.g., A + B * C), operators are placed between operands, which can be ambiguous without operator precedence and parentheses. To simplify evaluation, such expressions are often converted to postfix (e.g., A B C * +) or prefix notation (e.g., + A * B C) using stacks.
Conclusion
We have covered the implementation, complexity and analysis of stack operations. Stack is a versatile data structure that covers varied real life applications and because of that it is very easy to understand the representation of stack data structure.




![Top 10 Applications of Linked List Data Structure [2025]](https://www.iquanta.in/blog/wp-content/uploads/2025/02/WhatsApp-Image-2025-02-01-at-2.48.42-PM-218x150.jpeg)

